Archivos de autor para Arturo

Escala logarítmica, los sentidos y la bolsa

El principal uso de los logaritmos desde que John Napier los introdujo en el siglo XVII hasta nuestros tiempos, era como una herramienta que nos permitía realizar multiplicaciones con sumas. Esto gracias a la propiedad de los logaritmos que nos dice que log(ab) = log(a)+log(b) y unas inmensas tablas de logaritmos. Esto permitió simplificar mucho los tediosos cálculos necesarios en ingeniería, astronomía y ciencias en general. Más allá de este uso inicial, que ahora ya es mucho menos relevante, los logaritmos tienen propiedades muy interesantes que siguen haciéndolos imprescindibles en todas estas disciplinas. Una de ellas es la de nos presenta la ley de Weber-Fechner que nos dice como nuestros sentidos reescalan la magnitud de un estímulo físico para permitir que su percepción sea la adecuada, de forma mucho más tolerante a los extremos. Por ejemplo, podemos ver perfectamente las estrellas en mitad del campo y nos costará mucho más en la ciudad donde la contaminación lumínica hará cambiar nuestra escala de percepción. O lo mismo pasará si contestamos una llamada telefónica en nuestra casa o en mitad de una discoteca, donde nos será más difícil por no decir imposible. ¿Qué pasaría si nuestros sentidos mantuvieran una escala lineal de percepción? Pues que o bien serían aptos para identificar estímulos en la parte baja de la escala, siendo los estímulos de la parte alta insoportables, o bien serían aptos para soportar los estímulos de la parte alta, siendo imperceptibles los de la parte baja. De forma empirica Fechner dedujo que la percepción p de un estimulo S es proporcional al logaritmo de dicho estímulo entre el umbral a partir del cual dicho estímulo no es perceptible S_0.

p=k\ln \left ( \frac{S}{S0} \right )

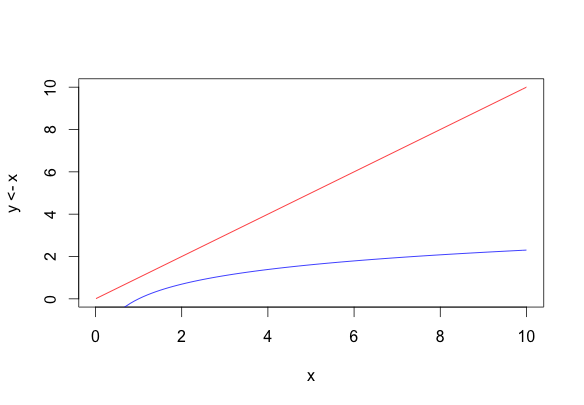
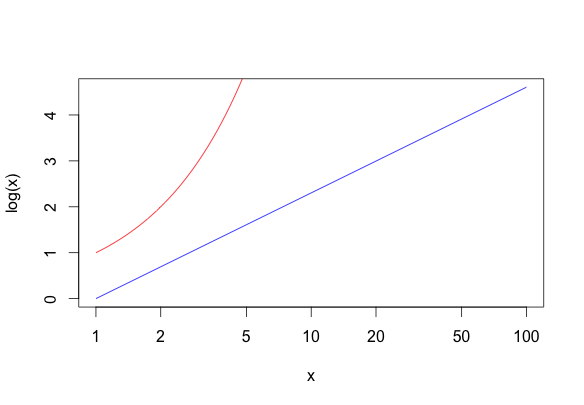
Siendo k una constante a calibrar empíricamente. Representando gráficamente la diferencia una función lineal y otra logarítmica utilizando ambas escalas podemos ver como el logaritmo de un estimulo con una escala logarítmica nos da la impresión de ser lineal, que es la percepción que tenemos de la realidad.

escala.lineal

Escala lineal

escala.log

Escala logarítmica

Y las funciones en R utilizadas para generar estas gráficas.

## Curvas y=x e y=log(x) con escala lineal
curve(y<-x, from = 0.01, to = 10, col = "red")
curve(log(x), from = 0.01, to = 10, add = TRUE, col = "blue")

## Curvas y=log(x) e y=x con escala logarítmica
curve(log(x), from = 1, to = 100, col = "blue", log="x")
curve(y<-x, from = 1, to = 100, add = TRUE, col = "red", log="x")

Derivando la ecuación anterior, podemos obtener como cambia la percepción respecto a un cambio en el estímulo.

\mathrm{d}p=k\frac{\mathrm{d}\mathrm{\left [ \ln\left ( S \right ) - \ln\left ( S_0 \right ) \right ]} }{\mathrm{d} S}

\mathrm{d}p=k\frac{\mathrm{d} S} {S}

¿Qué pasaría si extrapolásemos esta ley a la percepción del valor de un activo que tienen de los inversores ante su cambio en precio?. Esto ya se lo planteó MFM Osborne, siendo el primero en asociar el movimiento browniano al precio de las acciones, en un artículo de 1958, «Brownian motion in the stock market«.

En realidad esto es muy discutible, ya que supone que la percepción de un inversor sobre el valor real solo depende del precio del activo. Despreciando posibles eventos corporativos como los dividendos, publicación de resultados, cambios de gestión, etc.

Pero Osborne infiere la ley de Weber-Fechner a partir de los datos de cotizaciones publicados en NYSE y ASE.

dLogP

De hecho observa una distribución normal en los cambios de los logaritmos de los precios, es decir que los precios de los activos siguen una distribución lognormal. Lo que, como dice, sugiere que puede ser debido a que muchas variables aleatorias independientes contribuyen a estos cambios, como por otro lado parece lógico que ocurra.

Black-Scholes y la ecuación del calor

En 1973 Fischer Black y Myron Scholes publicaron un artículo, «The Pricing of Options and Corporate Liabilities» y ese mismo año Robert Merton publicó «Theory of rational option pricing» que pondría en auge el uso de los derivados y cambiaría la forma en la que se cotizan y gestionan sus riesgos.

Por esta aportación a las finanzas cuantitativas Scholes y Merton ganarían el premio Nobel de Economía en 1997, Black había muerto en el 95. Curiosamente en 1998, tan solo un año después de que ganasen el Nobel, quebraría el hedge fund LTCM (Long-Term Capital Management) a cuya junta directiva pertenecían Scholes y Merton, pero eso es otra historia.

El caso es que su aportación se suele resumir en la famosa ecuación de Black-Scholes pero cuyos principios son la base de lo que se conoce como teoría de replica.

Esta teoría postula que el precio de un derivado se puede calcular como el coste de su replica en mercado, esto bajo ciertas hipótesis, como la ausencia de arbitraje. Esta replica podemos verla como una cobertura dinámica y por lo tanto que anule los movimientos del valor del derivado en el tiempo.

Así pues podemos formular un portfolio riesgo neutro, compuesto por una posición larga en el derivado y otra corta en el subyacente, en una cuantía igual a la sensibilidad del derivado a movimientos en el subyacente.

d{\Pi}=dV_t - \frac{\partial{V_t}}{\partial{S_t}}dS_t

Y aquí ya necesitamos crear un modelo del mundo real, en este caso de la dinámica del subyacente y lo haremos con una ecuación diferencial estocástica. Suponemos además un comportamiento lognormal del subyacente, que en renta variable es razonable ya que no podemos tener precios negativos como tendríamos en una distribución normal.

{dS=\mu Sdt + \sigma SdW}

Dada la dinámica del subyacente y la composición del porfolio que depende de este subyacente, podemos aplicar el lema de Itô para desarrollar la siguiente ecuación diferencial.

d\Pi=\left[\frac{\partial{V_t}}{\partial{t}}dt+\frac{\partial{V_t}}{\partial{S_t}}dS_t+\frac{1}{2}\sigma^2S^2\frac{\partial^2{V_t}}{\partial{S_t^2}}dt\right]-\frac{\partial{V_t}}{\partial{S_t}}dS_t

La función que nos da la evolución de la cartera d\Pi depende de la función que nos da la evolución del subyacente dS que es de donde viene el termino estocástico. Podemos ver que, tal y como hemos conformado nuestro porfolio de replica, este término desaparece.

d\Pi=\frac{\partial{V_t}}{\partial{t}}dt+\frac{1}{2}\sigma^2S^2\frac{\partial^2{V_t}}{\partial{S_t^2}}dt

Este portfolio tiene como condición ser riesgo neutro así que su rendimiento debe de ser el tipo de interés libre de riesgo.

d{\Pi}=r\Pi dt

Y sustituyendo obtenemos la ecuación de black-scholes.

\frac{\partial{V_t}}{\partial{t}}dt+\frac{1}{2}\sigma^2S^2\frac{\partial^2{V_t}}{\partial{S_t^2}}dt+r\frac{\partial{V_t}}{\partial{S_t}}S-rV_t=0

A primera vista no es tan obvio su equivalencia con la ecuación del calor.

\frac{\partial{u}}{\partial{t}}=c^2\frac{\partial^2{u}}{\partial{x^2}}

Pero con los siguientes cambios de variables podemos transformar la ecuación de black-scholes en la ecuación del calor.

V=ue^{rT} => u=Ve^{-rT}

S=e^x => x=ln S

Con estos cambios de variables es donde podemos ver que la temperatura u en un instante de tiempo T en el punto x tendría su correspondencia con el valor descontado del derivado V para el precio del subyacente S.

Ahora bien, la solución de una ecuación diferencial depende de las condiciones de contorno que le pongamos. Que en la ecuación del calor podemos fijar por ejemplo que la temperatura en los extremos del segmento es cero.

u(0, t)=u(L, t)=0

Quedando la solución para la ecuación del calor.

u(x,t)=\sum_{n=1}^{\infty }B_ne^{-{\lambda}_nt}sinn\frac{\pi}{L}x

\lambda^2=c^2\left ( \frac{\pi}{L} \right )^2 y c^2=\frac{K}{\sigma \rho }

Donde L es la longitud, K la conductividad del material, \sigma el calor, \rho la densidad del material.

Y en black-scholes la condición de contorno vendrá dada por la propia definición del payoff, por ejemplo para una opción call.

V_T = max(0, S-K)

Quedando la solución para black-scholes.

C_t = S_tN(d_1)-Ke^{-r(T-t)}N(d_2)

Donde N es la distribución Normal estándar y d_1 y d_2

d_1=\frac{ln\left(\frac{S_t}{K}\right)+\left(r+\frac{1}{2}\sigma^2\right)(T-t)}{\sigma\sqrt{T-t}}

d_2=d_1-\sigma\sqrt{T-t}

A continuación podemos ver un gráfico animado donde se muestra la evolución de ambas soluciones en el tiempo.

diffusion.loop

En esta animación podemos ver como la difusión del calor nos lleva a un equilibrio en todos puntos del segmento, manteniendo las condiciones de contorno que fijaban la temperatura en los extremos.

Y el precio de la opción va perdiendo el valor temporal para ajustarse al valor intrínseco dado por la definición del payoff, que era la condición de contorno.

Y aquí tenéis el código en R que he utilizado para generar esta animación (utilizando la librería animation) y que implementa las soluciones a ambas ecuaciones.

Sys.setenv(PATH=paste(Sys.getenv("PATH"),"/opt/ImageMagick/bin/",sep=":"))
library(animation)
 
call <-
function(S, K, T, r, sig){
## S. precio del activo subyacente
## K. strike de la opcion
## T. tiempo para vencimiento
## r. tipo de interes
## sig. volatilidad implicita

  d1 <- (log(S/K) + (r + sig^2/2)*T) / (sig*sqrt(T))
  d2 <- d1 - sig*sqrt(T)

  value <- S*pnorm(d1) - K*exp(-r*T)*pnorm(d2)

  return(value)
}

callInstance <-
function(S, T){
	call(S, 10, T, 0.01, 1)
}

heat <-
function(x, K, T, r, sig){
## x. posicion
## K. conductividad del material en cal/cm sec
## T. tiempo
## r. densidad del material en gm/cm^3
## sig. calor en cal/gm

	B <- 5
	L <- 10
	c2 <- K / (r * sig)
	l2 <- c2 * (pi/L)^2
	
	value <- B * exp(-l2*T) * sin((pi/L)*x) 

	return(value)
}

heatInstance <-
function(x, T){
	heat(x, 0.9, T, 15, 0.1)
}

saveGIF({
  T <- 100
  while(T >= 0){
    curve(callInstance(x, T / 100), from = 0, to = 20, col = "blue", ylab = "")
    curve(5+heatInstance(x, 100-T), from = 0, to = 20, add = TRUE, col = "red", ylab = "")
    legend("topright", legend = c("call", "heat"), fill = c("blue", "red"), bty = "n")
    T <- T - 2
  }
}, interval = 0.1, ani.width = 550, ani.height = 350)